Standard Deviation of Linear Combination of Random Variables
You get standard deviations by calculating variances and then taking square roots at the end. To find the standard deviation take the square root of the variance formula.

Linear Combination Of Random Variables W 9 Examples
Q a22 X b22 Y Similarly the random variable D X Y follows X Y N X Y.
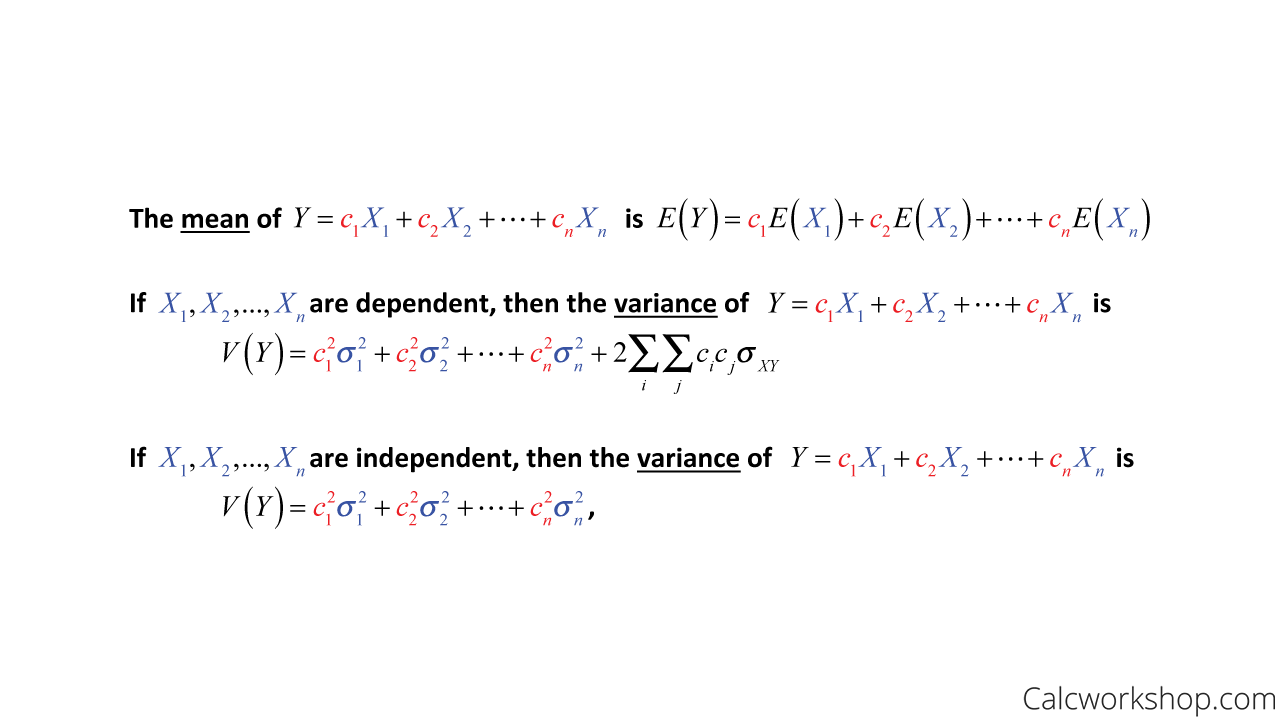
. Multiplying a random variable by a constant multiples its standard deviation by the absolute value of the constant. Q 2 X 2 Y. σ V 150σ X.
Variability of a linear combination of two independent random variables. Even when we subtract two random variables we still add their variances. The standard deviation of X is multiplied by 150 and is unchanged by the subtraction.
Second for each value in the group 45 40 25 and 12 subtract the mean from each and multiply the result by the probability of that outcome occurring. Combinations of random variables Now we want to look at what happens when we combine two data sets either by adding them or subtracting them. V aX bY a 2 V X b 2 V Y The standard deviation of the linear combination is the square root of the variance.
Mean Transformation For Continuous. For any two independent random variables X and Y if D X - Y the variance of D is D2 X-Y2x2Y2. E X i 2 E X i p.
Linear combinations of normal random variables. Standard deviation of linear combinations of random variables. V 5S 4C 5 2 V S 4 2 V C 25 15 2 16 2 2.
Make sure that the variables are independent or that its reasonable to assume independence before combining variances. If p 50 this is 1 6000 and the standard deviation is 1 6000 or about 13. Z X - μ σ where X is the value of the element μ is the mean of the population and σ is the standard deviation.
The z-score equation is given as. Random variables Jointly distributed random variables. We find the standard deviation of each and then we apply the equation for the standard deviation of the sum of two variables.
Effects of a Linear Transformation on the Mean and Standard Deviation If Y a bX is a linear transformation of the random variable X then. This article gives a geometric interpretation that views the standard deviation of a linear combination of random variables in terms of the length of the hypotenuse of a triangle and its calculation as equivalent to the theorem of Pythagoras. VarY sum_j1psum_k1pc_jc_ksigma_jk c prime Sigma c.
Var a X b Y c a 2 Var X b 2 Var Y 2 a b Cov X Y Independence implies 0 correlation so the second one comes up a lot. The random variable P is a linear combination of the random variables X and Y. 5625 64.
P 5X 5Y x y prob p 1 005 005 01 005 2 015 005 04 010 3 005 015 04 010. The mean of the linear combination is. Mean Sum and Difference of Two Random Variables.
When were combining multiple linear random variables we can find the mean and standard deviation of the combination using the means and standard deviations of the individual variables. Q a22 X b22 Y and aX bY N a X b Y. Use the formula or your calculator.
But when the random variables are combined in linear form the formula of the variance of the random variable that is obtained by combining random variables can be expressed as a simple sum of the variances of the variables involved and it also adds up the covariance of the variables involved in the combination. To calculate the di erence between 2 random variables we have a linear combination with a 1 1 and a 2 1 I want to calculate the toll revenue on SH-130 today. SD sqrt SDX2 SDY2.
The population variance of a linear combination is expressed as the following double sum of j 1 to p and k 1 to p over all pairs of variables. Up to 10 cash back Correct answer. The variance of the linear combination is 689 and the standard deviation is the square root of 689.
E3X_14X_23EX_14EX_2324318 and the variance of the linear combination is. We write XY N X Y. First calculate the mean of the random variables.
Multiplying a random variable by a constant multiples its standard deviation by the same constant. Linear combinations Distributions of Linear Combinations. Also aXbY N a X b Y.
Var X p 1 p 1500. Subtracting two variables increases the overall variability in the outcomes. For example if we let X be a random variable with the probability distribution shown below we can find the linear combinations expected value as follows.
Additionally this theorem can be applied to finding the expected value and variance of the sum or. X z σ 95 110 12 95 1082. Q a22 X b22 Y and aXbYc N a X b Y c.
Up to 10 cash back There are four steps to finding the standard deviation of random variables. Therefore Var X i p p 2 p 1 p. 3 Variance of a linear combination general.
The variance of the sample proportion is. If X 1 is the number of cars and X 2 the number of semi trucks the revenue is a 1X 1 a 2X 2 where a 1 and a 2 are the toll charged to each car and truck. The linear combination of two independent random variables having a normal distribution also has a normal distribution.
Third add the four results together. This logic generalizes to any linear transformation. Random variable S X Y follows also the normal distribution with mean X Y and standard deviation q 2 X 2 Y.
Q 2 X 2 Y. To solve for the students test score X. Linear combinations not only have a population mean but they also have a population variance.
Suppose X and Y have the joint distribution given below and w 1 w. Heres a few important facts about combining variances. By Marco Taboga PhD.
If X is a random variable and a b are non-random constants then beginalign textrmEaX b atextrmEX b textrmSDaX b atextrmSDX textrmVaraX b a2textrmVarX endalign. But why is the standard deviation so low. A property that makes the normal distribution extremely tractable from an analytical viewpoint is its closure under linear combinations.
Standard deviations do not add. Formally if X is a random variable and a b are non-random constants then beginalign textrmEaX b atextrmEX b textrmSDaX b atextrmSDX textrmVaraX b a2textrmVarX endalign. To find the standard deviation of a linear combination of random variables we first consider aX and bY separately.
So we will use the above formula to calculate the exercise.
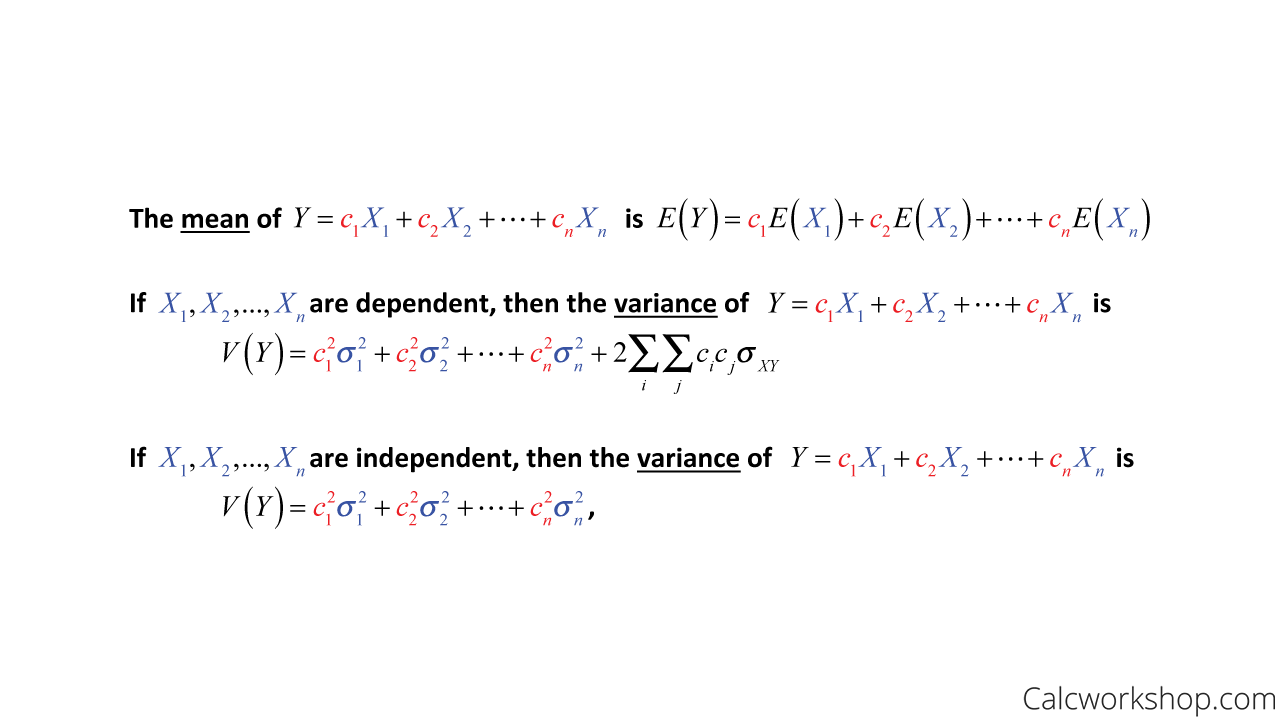
Linear Combination Of Random Variables W 9 Examples
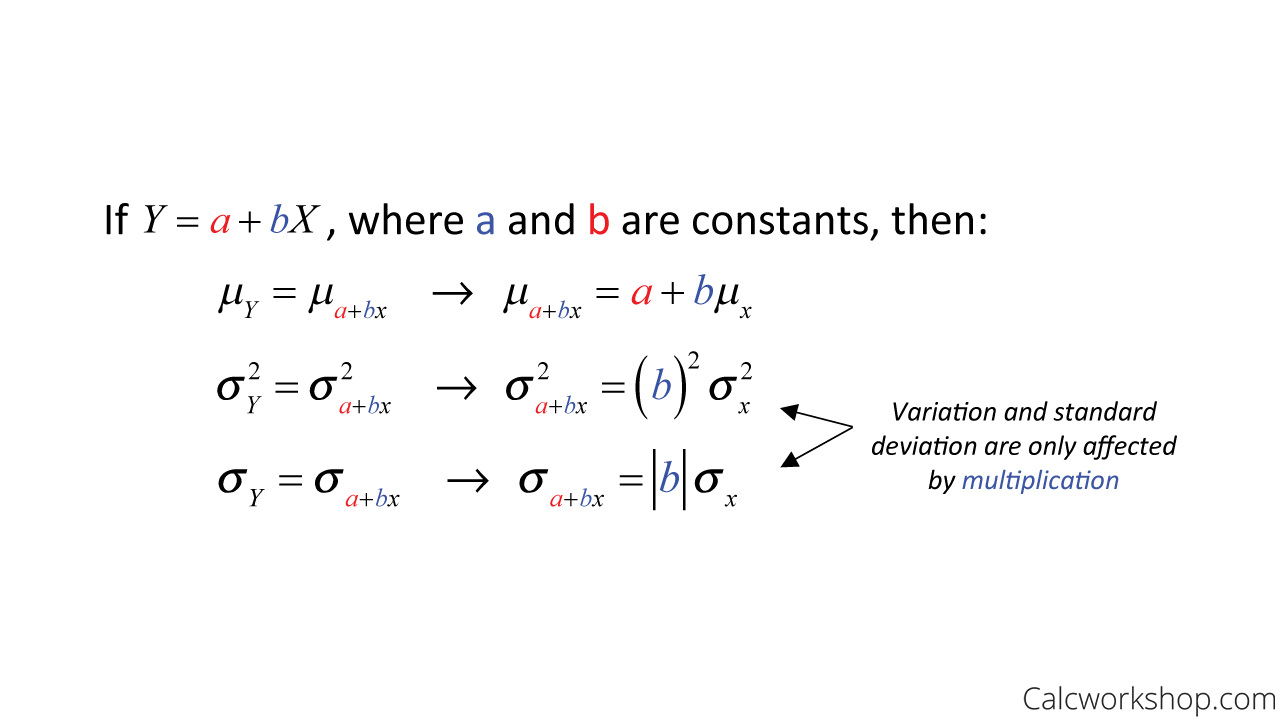
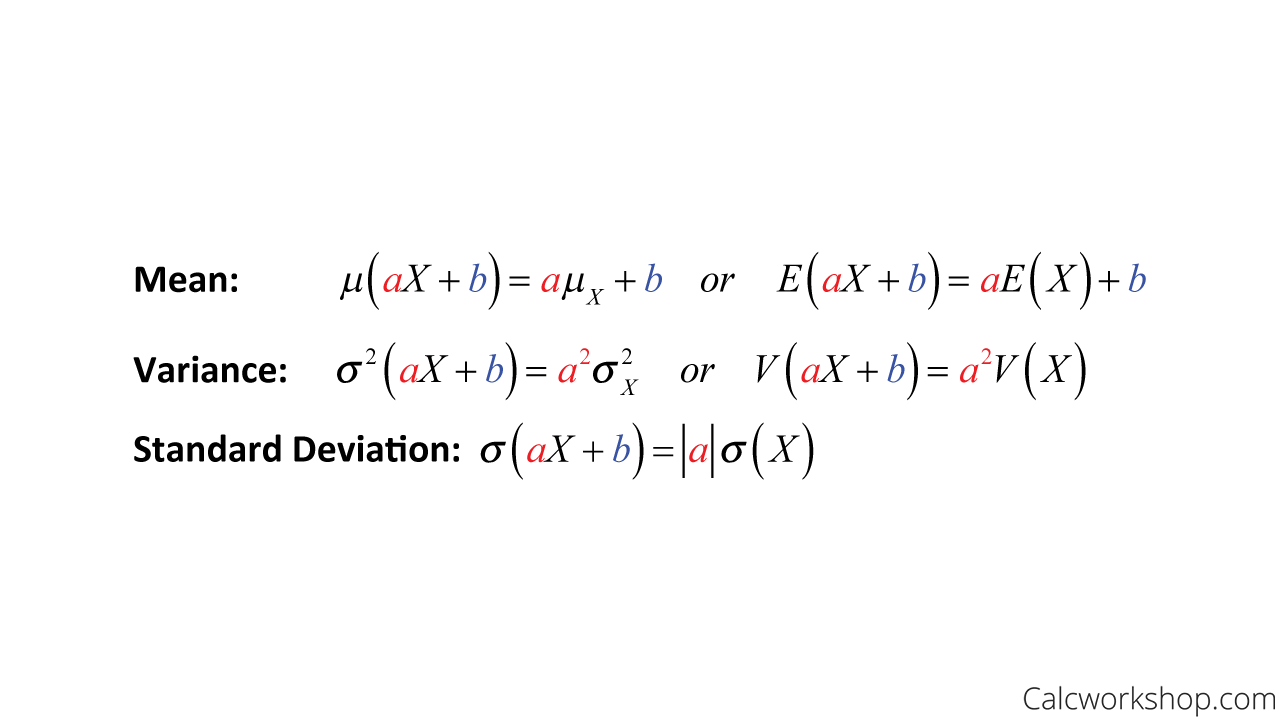
No comments for "Standard Deviation of Linear Combination of Random Variables"
Post a Comment